最終更新日 2024年11月14日
Diffie-Hellman鍵交換プロトコルでの共通鍵作成の流れは理解が難しい？
Diffie-Hellman鍵交換プロトコルは理解するのが難しいという声をよく聞きます。
特に数学が苦手な方や文系出身の方が苦手意識を持っていることが多いです。
数学が苦手な人がDiffie-Hellmanに対して苦手意識をもつのは、セキュリティやネットワークの知識だけでなく、数学の知識も必要になるためです。(共有鍵作成の際、modなどの数学的な処理をします。)
例えば共通鍵Kを計算する際の計算式は下記ですが、数学が苦手な人がこれを見ると理解する意欲をそがれてしまいます。
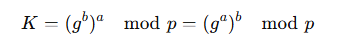
このように、様々な知識が必要になるため理解に至るまでに結構時間が掛かってしまう場合が多いです。
X(旧Twitter)では、以下のような投稿がされており、この投稿からもDiffie-Hellman鍵交換プロトコルの理解が難しいことが分かります。
現場の後輩エンジニアに「Diffie-Hellman鍵交換プロトコル」での共通鍵作成の流れを説明する際実施している指導手順
今回の記事では、私が現場で実践している、後輩エンジニアに「Diffie-Hellman鍵交換プロトコル」での共通鍵作成の流れを説明する際の指導手順を解説します。
Diffie-Hellmanでの公開鍵作成までの流れは以下の構成、4ステップで説明しています。
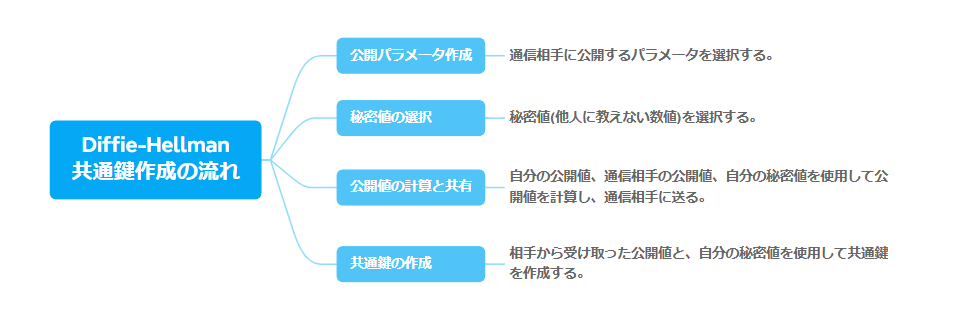
上記に加えて、まず最初にDiffie-Hellmanとは何かを概要レベルで説明するのが望ましいです。
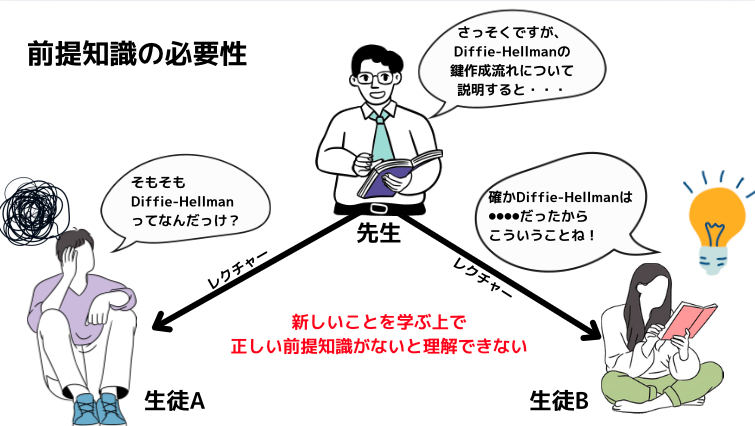
理由は、そもそもDiffie-Hellmanがどのような仕組みなのかという前提が理解されていないと、公開鍵の作成手順を説明しても正しく理解できないからです。
説明を進めていく中で、聞き手が自分の持っているDiffie-Hellmanの認識と違うことに気づくかもしれません。その場合、それまでの理解が誤解に基づいていた可能性があり、1から説明し直す必要が出てきます。
そのため、最初にDiffie-Hellmanの概要を共有し、認識を揃えておきましょう。
さらに、AさんとBさんを例にして、共通鍵ができるまでの各ステップでどんな計算が行われるのかを、実際の数値を使って説明するとより理解しやすくなります。
ステップ0 前提知識の認識合わせ
まずは、Diffie-Hellmanとはどのようなものなのか前提知識の認識を聞き手と合わせましょう。
理由については先ほど記載しました通り、Diffie-Hellmanとはどんなものなのか、聞き手と教える側の認識の不一致により、説明した内容を聞き手が正しく理解できない可能性があるからです。
Diffie-Hellmanについて認識合わせをする際は、最低限、「概要(どんなものか)」「理由(何のためにあるのか)」「目的(何ができるようになるのか)」を説明しましょう。
私はいつも以下のように説明しています。
Diffie-Hellmanとは、インターネット上などの公開された環境でも、安全に共通の暗号鍵を生成するためのアルゴリズム(特定の処理をするための一連の手順や計算方法)です。このアルゴリズムは、鍵を直接やりとりすることなく、互いに同じ共通鍵を作り出すためのものです。これにより、第三者に盗み見られることなく、安全に暗号化された通信を行うことが可能になります。
ステップ1 公開パラメータ作成
前提知識についての認識合わせが終わったら、「公開パラメータの作成」を説明しましょう。
「公開パラメータの作成」は以下の赤枠部分です。
このステップを説明する際、下記の3点を伝えるようにしましょう。
- 公開パラメータは何に使用されるか
- 公開パラメータはどのようなパラメータなのか
- 誰が公開パラメータを決めるのか
私はいつも以下のように説明しています。
公開パラメータは、通信者が共通鍵を作るための基盤となるものです。このパラメータは、共通鍵を計算する際の材料であり、ステップ3で公開する値を導き出す際にも使用されます。つまり、共通鍵を生成するための要素です。
公開パラメータは「素数」と「生成元」の2種類あり、これらは、どちらか一方が作成して相手に共有したり、通信者双方で合意して決めることもあります。
Aさん↔︎Bさんでの共通鍵作成 ステップ1
Aさんが以下公開パラメータをBさんに提案し、Bさんは公開パラメータが問題なければ合意します。
• 大きな素数 p = 23
• 生成元 g = 5
ここで、「素数 p 」は割り切れる数が1と自分(例の場合は23)だけの数、「生成元 g 」はこの後のステップの計算に使います。
ステップ2 秘密値の選択
次は「秘密値の選択」について説明しましょう。
「秘密値の選択」は以下の画像の赤枠部分です。
秘密値の選択については下記3点を伝えられるようにしましょう。
- 誰が秘密値を選択するのか
- 秘密値は何に使用されるのか
- 秘密値は他人に知られてはいけないこと
私はいつも以下のように説明しています。
秘密値は通信する両者がそれぞれ選びます。この秘密値は、ステップ3で公開値を計算するために使われます。もし秘密値が悪意のある人に知られてしまうと、共通鍵を作られてしまい、その共通鍵を使って暗号化されたデータを盗み見られる危険があります。そのため、秘密値は絶対に他人に教えてはいけない値です。
Aさん↔︎Bさんでの共通鍵作成 ステップ2
• Aさんは自分だけが知っている「秘密値 a = 6 」を選択
• Bさんは自分だけが知っている「秘密値 b = 15 」を選択
ステップ3 公開値の計算と共有
次は「公開値の計算と共有」について解説しましょう。
このステップは下記画像の赤枠部分です。
このステップでは以下の点を押さえて説明しましょう。
- 公開パラメータと秘密値で公開値を計算すること
- 両者の公開値はお互いに共有すること
- 公開値は公開しても問題ないこと
私はいつも以下のように説明しています。
次に、ステップ1と2で決めた公開パラメータと秘密値を使って公開値を計算します。この公開値は共通鍵を作るために必要なので、相手と共有します。この値は公開しても問題ありません。それでは、実際にどのような計算が行われるのかを見ていきましょう。
Aさん↔︎Bさんでの共通鍵作成 ステップ3
Aさんの計算
Aさんは「生成元 g = 5 を秘密値 a = 6 乗して、それを p = 23 で割った余り」を計算します。
計算式： (5の6乗) ÷ 23
5の6乗 = 15625
15625 ÷ 23 = 679 余り 17
Aさんの公開値は17です。
Bさんの計算
Bさんは「生成元 g = 5 を秘密の数 b = 15 乗して、それを p = 23 で割った余り」を計算します。
計算式： (5の15乗) ÷ 23
5の15乗 = 30517578125
30517578125 ÷ 23 = 1326863788 余り 19
Bさんの公開値は19です。
この公開値（17と19）は、インターネットなどで公開しても問題ありません。
ステップ4 共通鍵の作成
次は実際に共通鍵を作成するステップについて解説しましょう。
このステップは画像ていうところの以下赤枠部分です。
このステップでは以下のポイントを押さえて説明しましょう。
- 相手の公開値、公開パラメータ、自分の秘密値で共通鍵を計算する
- お互いの共通鍵の計算結果は一致する
- 共通鍵が同じ値になるので通信の際お互いにデータを復号できる
私はいつも以下のように説明しています。
このステップでは、相手の公開値、公開パラメータ、自分の秘密値を使って共通鍵を計算します。この計算の結果、お互いが同じ共通鍵を得ることができます。この共通鍵を使ってデータの暗号化や復号を行い、通信を暗号化できるようになります。
それでは、具体的にどのような計算が行われているのか見てみましょう。
Aさん↔︎Bさんでの共通鍵作成 ステップ4
Aさんの共通鍵の計算
AさんはBさんから受け取った公開値19 を使って、「Bさんの公開値を自分の秘密の数 a = 6 乗して、それを p = 23 で割った余り」を計算します。
計算式： (19の6乗) ÷ 23
19の6乗 = 47045881
47045881 ÷ 23 = 2045473 余り 2
Aさんの共通鍵は2です。
Bさんの共通鍵の計算
BさんはAさんから受け取った公開数 17 を使って、「Aさんの公開数を自分の秘密の数 b = 15 乗して、それを p = 23 で割った余り」を計算します。
計算式： (17の15乗) ÷ 23
17の15乗 = 437893890380859375
437893890380859375 ÷ 23 = 19038864712120825 余り 2
Bさんの共通鍵も2です。
AさんもBさんも、計算の結果同じ共通鍵 2 を得ました。
この共通鍵2を使用して通信を暗号化、復号化します。
まとめ
最後に余力があれば、これまで説明した共通鍵作成手順をまとめましょう。
その際は、以下のポイントを押さえて説明すると分かりやすいです。
- 共通鍵完成までのざっくりとした流れ
- 共通鍵作成に必要な材料
私はいつも以下のように説明しています。
最後に、共通鍵が作られる流れをおさらいしましょう。共通鍵は4つのステップで作成されます。1つ目は「公開パラメータの作成」、2つ目は「秘密値の選択」、3つ目は「公開値の計算」、そして4つ目は「共通鍵の作成」です。共通鍵を作るためには、公開パラメータ、公開値、そして秘密値が必要です。
具体的な例として使用した、AさんとBさんの共通鍵作成時に使われた値は次の通りです。
公開値: 素数 p = 23 、生成元 g = 5 、Aさんの公開数 17 、Bさんの公開数値 19
秘密値: Aさんの秘密値 a = 6 、Bさんの秘密値 b = 15
最終的にAさんとBさんが計算した共通鍵: 2
Diffie-Hellmanによる共通鍵の作成の流れを理解するメリット
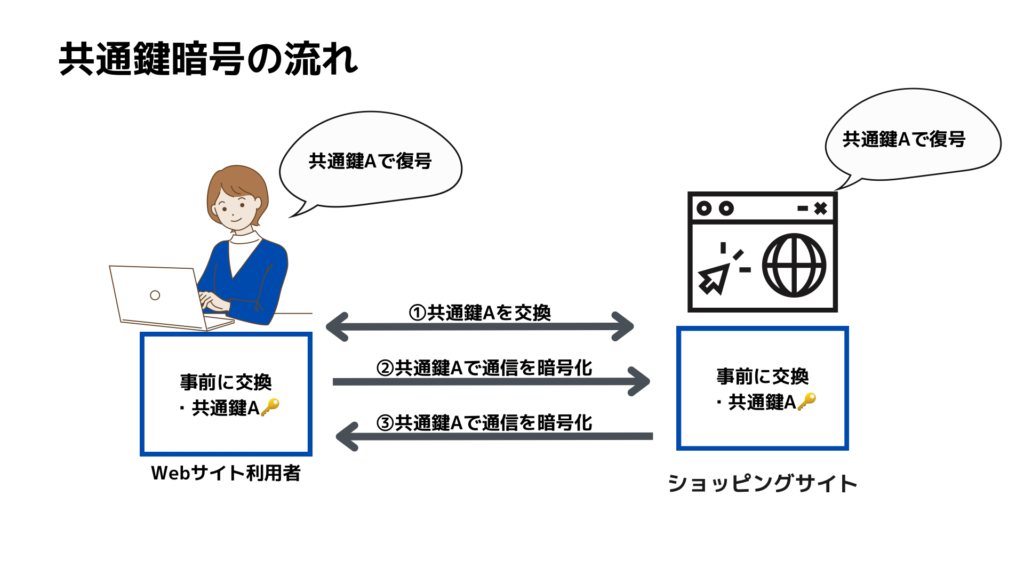
Diffie-Hellmanによる共通鍵の作成の流れを理解することで、安全な通信の仕組みが分かるようになります。特に、日常で使っているインターネットのやり取り（例えば、オンラインショッピングやメッセージアプリ）がどのように守られているかを知ることができます。
Diffie-Hellmanは、通信データをが暗号化れていないにもかかわらず、通信相手だけと秘密裏に共通鍵を交換できる方法です。この仕組みを理解することで、「どうして外部の人が簡単に盗み見できないのか？」が見えてきます。セキュリティの基本を知ることは、自分自身をネット上の脅威から守るためにもとても大切です。